Квадратные уравнения – это математические выражения, которые часто возникают в различных ситуациях нашей повседневной жизни. Они помогают решать широкий спектр задач, связанных с физикой, инженерией, экономикой, а также во многих других областях.
Одна из главных областей, где квадратные уравнения находят практическое применение, – это физика. В задачах связанных с движением, квадратные уравнения позволяют найти решение для времени, расстояния и скорости. Например, квадратное уравнение может быть использовано для определения времени падения предмета с высоты, зная его начальную скорость и ускорение свободного падения.
Квадратные уравнения также являются неотъемлемой частью различных инженерных расчетов и моделирования. Они используются для определения оптимальных параметров в различных конструкциях, таких как мосты, здания и мостовые краны.
Квадратные уравнения обеспечивают также практическую пользу в экономических задачах. Они позволяют рассчитать различные финансовые параметры, такие как прибыль, потери, амортизацию и др., что помогает предсказать и оптимизировать результаты бизнес-процессов.
Учебные задачи с использованием квадратных уравнений

Рассмотрим несколько учебных задач, которые могут быть решены с использованием квадратных уравнений:
| Задача | Описание |
|---|---|
| 1 | Найти длину и ширину прямоугольного поля, зная его площадь и отношение сторон. |
| 2 | Выяснить, какое количество товара нужно продать, чтобы достичь определенного уровня прибыли при заданной цене и затратах. |
| 3 | Определить, через какое время два пешехода, отправившихся друг за другом из разных точек, встретятся, зная их начальные позиции и скорости. |
| 4 | Решить кинематическую задачу, связанную с движением тела под действием силы тяжести. |
| 5 | Найти максимальную или минимальную точку функции, заданной квадратным уравнением, при заданных ограничениях. |
Это лишь некоторые примеры задач, которые можно решить с использованием квадратных уравнений. Формула для нахождения корней квадратного уравнения позволяет найти точные значения неизвестных, а это важно для многих практических ситуаций. Поэтому знание и умение применять квадратные уравнения оказывается полезным и в повседневной жизни.
Расчет площади и периметра прямоугольных участков земли
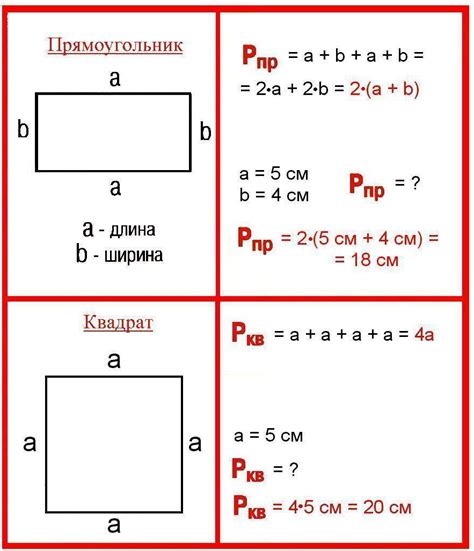
В повседневной жизни мы часто сталкиваемся с задачами, связанными с расчетом площади и периметра прямоугольных участков земли. Например, при покупке или продаже земельного участка, при строительстве дома или огорода. Знание квадратных уравнений поможет нам быстро и точно решить подобные задачи.
Площадь прямоугольника можно вычислить, зная длину (a) и ширину (b) его сторон. Формула для расчета площади прямоугольника: S = a * b. Найдя значения a и b, мы можем легко найти площадь участка земли.
Например, предположим, что у нас есть прямоугольный участок земли с длиной 10 метров и шириной 5 метров. Для расчета его площади мы умножим эти значения: S = 10 * 5 = 50 квадратных метров. Таким образом, площадь участка земли равна 50 квадратных метров.
Периметр прямоугольника может быть также вычислен, зная длину (a) и ширину (b) его сторон. Формула для расчета периметра прямоугольника: P = 2 * (a + b). Найдя значения a и b, мы можем легко найти периметр участка земли.
Продолжая предыдущий пример, допустим, что у нас есть прямоугольный участок земли с длиной 10 метров и шириной 5 метров. Для расчета его периметра мы используем формулу: P = 2 * (10 + 5) = 30 метров. Таким образом, периметр участка земли равен 30 метров.
Использование квадратных уравнений при расчете площади и периметра прямоугольных участков земли позволяет нам получить точные и надежные результаты. Эти знания пригодятся в различных ситуациях, связанных с покупкой, продажей или использованием земельных участков.
Определение дальности полета снаряда
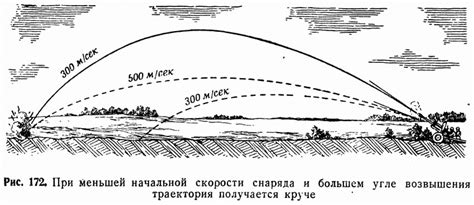
Когда снаряд выпускается под углом к поверхности земли, его полет можно описать квадратным уравнением. Это уравнение может помочь нам определить дальность полета снаряда в зависимости от начальной скорости и угла запуска.
Для решения этой задачи, мы можем использовать следующее квадратное уравнение:
d = (u^2 * sin(2θ))/g
Где:
- d - дальность полета снаряда
- u - начальная скорость снаряда
- θ - угол запуска снаряда
- g - ускорение свободного падения (приближенное значение 9.8 м/с^2)
Используя это уравнение, мы можем определить дальность полета снаряда при определенных начальной скорости и угле запуска. Это может быть очень полезно при разработке оружия, планировании трассы полета ракеты или даже при игре в гольф.
Таким образом, квадратные уравнения имеют реальное практическое применение в повседневной жизни, включая определение дальности полета снаряда. Их использование позволяет нам решать различные задачи, связанные с физикой и инженерией.
Моделирование траектории полета мяча
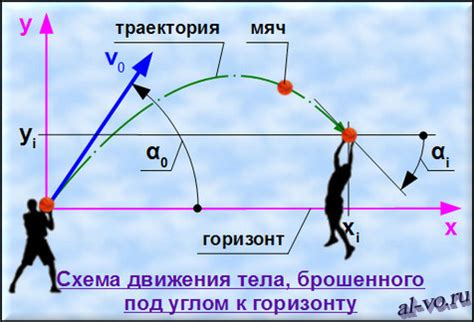
Представим, что у нас есть мяч, который мы бросаем в воздух. Чтобы предсказать его траекторию полета, мы можем использовать квадратное уравнение, которое описывает движение тела под действием силы тяжести.
Квадратное уравнение имеет вид:
y = ax^2 + bx + c
Где:
- y - вертикальная координата мяча на определенном времени,
- x - горизонтальная координата мяча на определенном времени,
- a, b, c - коэффициенты, которые зависят от физических параметров системы.
Используя известные значения коэффициентов и начальные условия (например, начальные координаты и скорость броска), мы можем решить квадратное уравнение и получить уравнение траектории полета мяча.
Таким образом, моделирование траектории полета мяча с использованием квадратных уравнений позволяет нам предсказать его движение и определить, где мяч будет находиться в определенный момент времени. Это может быть полезно, например, при разработке спортивных тренажеров или в физическом образовании.
Квадратные уравнения находят широкое применение в повседневной жизни, включая моделирование траектории полета мяча. Они позволяют нам предсказывать движение объектов и использовать это знание для различных целей, от разработки технических устройств до улучшения спортивных навыков.
Расчет времени падения тела

Квадратные уравнения могут быть использованы для расчета времени падения тела. Это может быть полезно, например, при определении времени, за которое объект упадет с определенной высоты или при предсказании момента падения объекта.
Рассмотрим пример. Пусть у нас есть объект, который падает с высоты h. Мы можем использовать формулу для свободного падения тела:
$h = \frac{1}{2}gt^2$
Где g - ускорение свободного падения (приближенно равное 9.8 м/с^2), t - время падения.
Чтобы решить это квадратное уравнение относительно времени, мы можем привести его к стандартному виду:
$0.5gt^2 - h = 0$
Далее мы можем использовать известную формулу для нахождения корней квадратного уравнения:
$t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
В нашем случае a = 0.5g, b = 0 и c = -h. Подставляя эти значения в формулу, мы можем вычислить время падения.
Найденные значения времени могут быть использованы для различных задач, связанных с падением тела. Например, они могут помочь определить, будет ли объект упадет в определенный момент времени или на расстоянии от точки падения.
| Пример: | Время падения (секунды) |
|---|---|
| Высота 10 м | 1.43 |
| Высота 20 м | 2.02 |
| Высота 30 м | 2.45 |
Таким образом, квадратные уравнения применяются не только в математике, но и в повседневной жизни, чтобы решить практические задачи, такие как расчет времени падения тела.
Нахождение начальной скорости движения автомобиля
Квадратные уравнения находят применение в повседневной жизни во многих областях, включая физику и инженерию. В данном случае они могут быть использованы для рассчета начальной скорости автомобиля.
Допустим, у вас есть информация о расстоянии, которое автомобиль должен пройти, и время, за которое это расстояние было преодолено. Также известно, что движение автомобиля происходило с постоянным ускорением.
Квадратное уравнение, связанное с этой ситуацией, может быть записано следующим образом:
s = ut + 0.5at^2
Где:
- s - расстояние, которое автомобиль прошел
- u - начальная скорость автомобиля
- t - время, за которое автомобиль преодолел данное расстояние
- a - ускорение автомобиля
Вы можете использовать это уравнение для вычисления начальной скорости автомобиля (u), если известны значения s, t и a.
Для этого вам понадобится решить квадратное уравнение, привести его к стандартному виду и применить формулу для нахождения корней квадратного уравнения:
u = (-b +/- sqrt(b^2 - 4ac)) / 2a
Где:
- b = t
- a = 0.5a
- c = -s
Решив это квадратное уравнение, вы найдете два значения для начальной скорости автомобиля (u), одно из которых может быть применимо в данной ситуации.
Таким образом, использование квадратных уравнений позволяет нам рассчитать начальную скорость движения автомобиля, основываясь на известных значениях расстояния, времени и ускорения.



