Теорема Пифагора – одно из самых известных математических положений, которое связывает длины сторон прямоугольного треугольника. Но почему же эта теорема в некоторых странах получила прозвище «теоремы невесты»? Существует несколько легенд, объясняющих происхождение этого любопытного названия.
Одна из версий связана с античностью и древнегреческим математиком Пифагором, которому приписывается открытие этой теоремы. По легенде, Пифагор и его ученики занимались изучением геометрии и весьма основательно. Их усердие было столь большим, что Пифагор запретил своим ученикам вступать в брак до тех пор, пока они не сделают себе совершенно белую одежду. Таким образом, когда ученик успешно освоил теорему Пифагора и получил его благословение, он мог наконец вступить в брак и надевать белое. Поэтому теорему назвали «теоремой невесты» в память о том, что ее владение позволяло им вступить в брак.
Существует и другая версия происхождения названия. Она связана с морскими путешествиями. При наступлении наемного века, когда мореплаватели отправлялись в далекие и опасные походы, их жены и подруги провожали мужей красивыми квилтами – одеяльцами из пяти кусочков ткани, каждый из которых символизировал одного из учеников Пифагора. Первый кусочек был белым, второй – красным, третий – фиолетовым, четвертый – темно-синим, а пятый – голубым. При каждом успешном плавании к пятицветному одеяльцу добавлялся новый кусочек ткани. Таким образом, вся пятнадцатая часть одеяльца засчитывалась морякам перед бракосочетанием. Именно поэтому теорему Пифагора назвали «теоремой невесты», ведь благодаря ее применению, геометрия помогала сделать возвращение мореплавателей безопасным, и им предоставлялось право на брак.
История открытия теоремы Пифагора

Согласно легенде, сам Пифагор, древнегреческий философ и математик, не считал свою теорему важной и не обращал на нее особого внимания. Один из его учеников считал ее гораздо более значимой и решил показать ее удивительные свойства своей невесте.
Идея заключалась в том, чтобы закрепить прямоугольный треугольник на поле, состоящем из разноцветных квадратных карточек. Каждый квадрат представлял собой квадрат гипотенузы или катетов соответствующего размера. После этого, невесте нужно было расставить квадраты в правильном порядке и собрать картину.
Когда невеста справилась с заданием, ученик Пифагора объяснил ей, что кроме задачи решить прямоугольный треугольник, она только что доказала теорему Пифагора. Невеста была потрясена и восхищена этим открытием, и с тех пор теорему начали называть "теоремой невесты".
С течением времени, термин "теорема невесты" стал популярным и известным, в то время как имя самого Пифагора стало ассоциироваться с его учеником-самозванцем. Тем не менее, история открытия теоремы Пифагора остается важной частью математической и культурной наследии.
Кто был Пифагор и как он пришел к открытию теоремы?

Известно, что Пифагор и его последователи открыли много важных математических закономерностей и теорем, но, пожалуй, самой знаменитой стала теорема Пифагора. Он сформулировал ее, основываясь на наблюдениях и экспериментах с прямоугольными треугольниками.
Суть теоремы Пифагора заключается в следующем: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Или, с математической точки зрения:
- Гипотеза: В прямоугольном треугольнике с катетами a и b и гипотенузой c выполняется равенство a² + b² = c².
- Доказательство: Пифагор использовал различные геометрические и алгебраические методы, чтобы доказать эту теорему.
Именно благодаря открытию этой теоремы Пифагор и его последователи добились больших успехов в астрономии, геометрии, музыке и философии. В их школе числа считались основой мироздания и ключом к пониманию всего сущего.
Почему именно эта теорема получила прозвище "теорема невесты", до сих пор остается загадкой. Возможно, это связано с тем, что она является одной из основных и самых известных теорем в математике, также она часто применяется в практике и имеет множество применений.
Применение теоремы Пифагора в геометрии
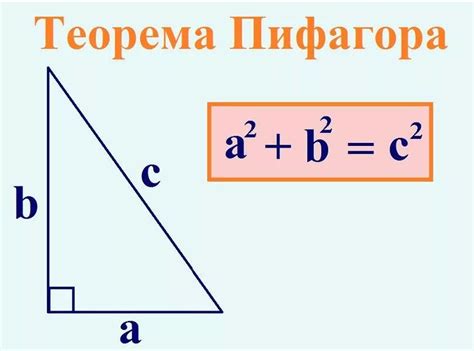
Одним из основных применений теоремы Пифагора является вычисление длины гипотенузы прямоугольного треугольника. Для этого достаточно знать длины двух других сторон. Также, зная длину гипотенузы и одной из катетов, можно вычислить длину второго катета.
Теорема Пифагора также применяется для определения, является ли треугольник прямоугольным. Если квадрат длины гипотенузы равен сумме квадратов длин двух других сторон, то треугольник является прямоугольным.
Более того, теорема Пифагора позволяет решать различные задачи на построение геометрических фигур. Например, с ее помощью можно построить проекцию точки на плоскость или определить расстояние между двумя точками.
Таким образом, теорема Пифагора имеет множество практических применений в геометрии и является одной из основных теорем, которую необходимо знать и уметь применять в решении различных геометрических задач.
Значение теоремы Пифагора для треугольников
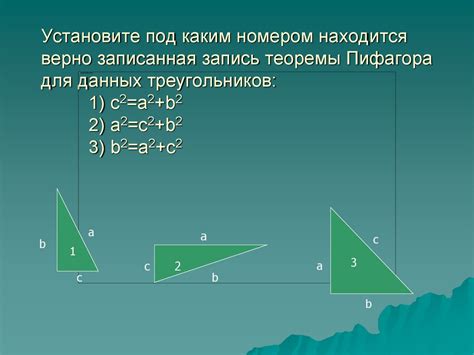
Теорема гласит: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Формально это записывается как a2 + b2 = c2, где a и b - длины катетов, а c - длина гипотенузы.
Теорема Пифагора имеет множество практических применений и значима для треугольников. Она позволяет вычислять неизвестные стороны или углы, а также проверять, является ли треугольник прямоугольным.
Зная две известные стороны прямоугольного треугольника, можно с помощью теоремы Пифагора вычислить длину третьей стороны. Это особенно полезно, когда требуется определить размеры недоступных объектов или провести диагональные линии на плоскости.
Теорема Пифагора также помогает в геометрических задачах, связанных с расчетом площадей треугольников. Зная две стороны треугольника, можно вычислить площадь с помощью теоремы Пифагора и формулы для площади треугольника. Это значительно упрощает решение задач, связанных с построением и геометрией треугольников.
Теорема Пифагора является основой для доказательств других важных свойств и теорем в геометрии. Она играет ключевую роль в понимании прямоугольных треугольников и их свойств. Научившись применять ее, можно значительно упростить и ускорить решение задач, связанных с треугольниками.
Теорема Пифагора в практических применениях

Одним из наиболее очевидных применений теоремы Пифагора является вычисление длин сторон прямоугольного треугольника. Если известны длины двух сторон треугольника, то теорема Пифагора позволяет легко найти длину третьей стороны. Это особенно полезно в проектировании и строительстве, где необходимо точно определить размеры и углы треугольника.
Теорема Пифагора также находит применение в решении задач связанных с электроникой и физикой. Например, для вычисления сопротивления в электрической цепи, с помощью правила Пифагора можно определить длину диагонали в прямоугольном треугольнике, где катеты соответствуют сопротивлениям в цепи.
Другие практические применения теоремы Пифагора включают вычисление расстояний между точками на координатной плоскости, определение площадей и объемов геометрических фигур, а также решение задач из оптики, астрономии и других областей естественных наук.
Таким образом, теорема Пифагора имеет широкий спектр практических применений и является важным инструментом для решения задач, требующих вычислений длин, площадей и объемов в различных областях знания.
Альтернативные названия теоремы Пифагора
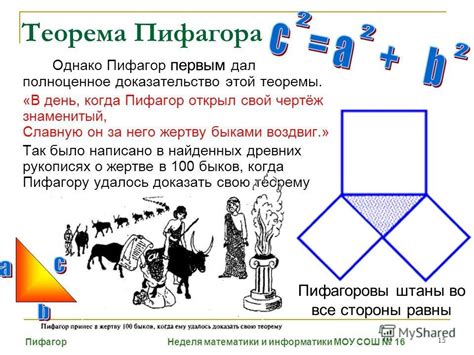
Теорема Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, имеет не только свое официальное название, но и несколько альтернативных названий.
Одно из таких названий - "Теорема Пифагора-Невесты". Вероятно, это связано с тем, что в повседневной жизни молодой человек часто стремится подарить своей избраннице нечто прекрасное и необычное. Таким образом, теорема Пифагора, с ее простотой и одновременной величественностью, символизирует подарок, способный удивить и поразить своей гармонией и непредсказуемостью.
Еще одно название этой теоремы звучит так - "Теорема Пифагора-Золушки". Возможно, данное название связано с тем, что в сказке о Золушке, она стала благодаря тому, что она оказалась единственной, чья ступня поместилась в стеклянную туфельку. Точно так же, теорема Пифагора - это нечто особенное, уникальное и неповторимое, что отделяет ее от множества других теорем и закономерностей.
Существуют и другие неформальные и менее привычные названия этой теоремы, которые употребляются в различных школах, странах и кругах, но они не имеют такой широкой известности, как "Теорема Пифагора-Невесты" или "Теорема Пифагора-Золушки".
Обращение к теореме Пифагора в культуре и искусстве

Теорема Пифагора, которая устанавливает соотношение между длинами сторон прямоугольного треугольника, имеет глубокое значение не только в математике, но и в культуре и искусстве. Её уникальность и универсальность сделали её источником вдохновения для многих великих музыкантов, художников, писателей и прочих творческих личностей, которые нашли отражение теоремы в своих произведениях.
В музыке многие композиторы вдохновлялись отношениями, выраженными в теореме Пифагора, чтобы создавать гармоничные и приятные слуху мелодии. Пифагорейцы верили, что созвучие звуков имеет математическую основу, и это привело к развитию науки о музыке. Пётр Чайковский в своих произведениях использовал гармонию и мелодические структуры, основанные на пропорциях и отношениях, а Вольфганг Амадей Моцарт удивительно точно применял теорему в своих симфониях и концертах.
В искусстве теорема Пифагора часто используется в композиции и пропорциях. Идеальное соотношение сторон, которое образуется в прямоугольном треугольнике, является основополагающим принципом в создании гармоничных и сбалансированных произведений искусства. Многие скульпторы, архитекторы и дизайнеры в своём творчестве тщательно следят за пропорциями, которые соответствуют теореме Пифагора, чтобы достичь эстетического совершенства.
Теорема Пифагора также имеет глубокий смысл и в философии и литературе. Её принципы о сбалансированности, гармонии и симметрии подтверждаются в произведениях многих философов и писателей. Философы античности, такие как Платон и Пифагор, использовали теорему для обоснования своих учений. Современные писатели, такие как Умберто Эко, Матиссе Депари, также нашли вдохновение в принципах, выраженных в теореме Пифагора, и применили их в своих книгах и исследованиях.
Таким образом, теорема Пифагора не только является фундаментальным математическим принципом, но и вдохновляет искусство и культуру, придаёт им гармонию и сбалансированность. Её применение в музыке, искусстве, философии и литературе подчёркивает её универсальность и вечность.



