Параллельные прямые – это математическое понятие, которое имеет широкое применение в различных сферах нашей жизни. Они играют важную роль в архитектуре, строительстве, технике и даже спорте. Понимание прикладного значения параллельных прямых помогает нам решать задачи и строить объекты с высокой степенью точности и симметрии.
В архитектуре параллельные прямые используются для создания гармоничных и сбалансированных конструкций. Архитекторы и дизайнеры используют параллельные линии, чтобы создать ощущение равновесия и порядка. Например, при проектировании зданий, таких как мосты, высокие небоскребы или дома, используются параллельные линии, чтобы создать структуру, которая выглядит устойчивой и эстетически привлекательной.
В строительстве и технике использование параллельных линий также играет важную роль. Например, при строительстве дороги необходимо, чтобы две параллельные линии были постоянного расстояния друг от друга, чтобы обеспечить безопасность движения автомобилей. Точность при измерениях и установке конструкций также требует использования параллельных прямых.
В спорте параллельные прямые используются для создания поперечных маркеров на спортивных полях, таких как футбольные или хоккейные поля. Эти маркеры помогают судьям и игрокам определить правильное положение и расстояние, а также следить за правильностью положения игровых элементов. Благодаря параллельным линиям достигается справедливая игра и обеспечивается фэйр-плей.
Таким образом, понимание прикладного значения параллельных прямых является важным для решения задач в различных областях. Они помогают нам создавать красивые и функциональные архитектурные сооружения, обеспечивать безопасность в строительстве и технике, а также справедливость в спорте.
Применение параллельных прямых в архитектуре

Параллельные прямые имеют важное прикладное значение в архитектуре. Они используются для создания эстетически приятных и гармоничных пространств в зданиях и сооружениях.
Одним из способов использования параллельных прямых в архитектуре является создание перспективных эффектов. Архитекторы могут использовать параллельные линии, чтобы создать иллюзию глубины и расширить пространство. Например, параллельные прямые на полу или потолке могут добавить ощущение простора и высоты.
Кроме того, параллельные прямые сами по себе могут служить декоративным элементом в архитектуре. Они могут использоваться для создания узоров на стенах, полах или потолках, что добавляет стиль и элегантность в интерьеры зданий.
Еще одним применением параллельных прямых является использование их в геометрическом планировании зданий. Архитекторы могут использовать параллельные прямые для выравнивания и разделения пространств, создания ориентира и подчеркивания архитектурных деталей.
Особенности и преимущества применения параллельных прямых в проектировании зданий
Одной из особенностей параллельных прямых является то, что они никогда не пересекаются. Это позволяет добиться правильной геометрии здания и создать четкие линии и углы. Благодаря параллельным прямым, архитекторы могут точно определить рамки и форму здания, учитывая его функциональность и эстетическое воздействие.
Преимущества использования параллельных прямых в проектировании зданий включают:
- Точность: Важным аспектом при проектировании здания является точное расположение стен, потолков, полов и других элементов. Использование параллельных прямых позволяет с легкостью поддерживать геометрическую правильность и точность всех составляющих здания.
- Удобство: Параллельные прямые являются интуитивным инструментом, который позволяет архитекторам и инженерам легко определить границы здания и его различные помещения. Их использование делает процесс проектирования более понятным и удобным.
- Эстетика: Параллельные прямые помогают создать гармоничный дизайн здания, образуя четкие и симметричные линии. Такое использование геометрической прямой не только способствует эстетической привлекательности здания, но и создает ощущение упорядоченности и профессионализма.
Применение параллельных прямых в геометрии

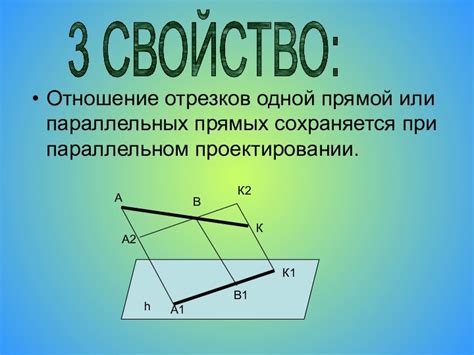
Во-первых, параллельные прямые используются для измерения углов. Когда две пересекающиеся прямые образуют две пары соответственных углов, то параллельные прямые образуют равные соответственные углы. Это позволяет измерять углы и определять их свойства.
Во-вторых, параллельные прямые применяются при построении и измерении геометрических фигур. Например, параллельные прямые используются при построении прямоугольников и параллелограммов. Измерение расстояния между параллельными прямыми позволяет определить ширину и высоту фигуры.
Кроме того, параллельные прямые играют важную роль в евклидовой геометрии. Одна из ее аксиом гласит, что через любую точку можно провести только одну прямую, параллельную данной. Это принцип имеет множество применений в геометрии, а также в технике и архитектуре.
Таким образом, параллельные прямые имеют широкое применение в геометрии. Они позволяют измерять углы, строить и измерять геометрические фигуры, а также являются основой для многих геометрических принципов и теорем.
Примеры использования параллельных прямых в решении геометрических задач

Параллельные прямые представляют собой основной инструмент для решения множества геометрических задач. Они находят применение в различных областях, от строительства до компьютерной графики. Ниже приведены несколько примеров использования параллельных прямых в решении различных геометрических задач.
Построение параллельных прямых через заданную точку.
Если дана точка и одна параллельная прямая, то можно построить параллельную прямую через заданную точку. Для этого необходимо построить перпендикуляр к данной прямой, проходящий через заданную точку, а затем провести параллель через эту точку.
Построение параллелограмма.
Для построения параллелограмма необходимо провести две параллельные прямые, соединить концы этих прямых отрезками и построить вторую пару параллельных прямых, проходящих через противоположные вершины параллелограмма.
Нахождение высоты в треугольнике.
Если в треугольнике проведены две параллельные прямые, то можно найти высоту треугольника как перпендикуляр к данным параллельным прямым, проходящий через оставшуюся вершину.
Построение треугольника по трем параллельным прямым.
Если даны три параллельные прямые, то можно построить треугольник, принимая эти прямые за стороны треугольника.
Это лишь несколько примеров использования параллельных прямых в геометрии. Параллельные прямые являются мощным инструментом для решения самых разнообразных задач и широко применяются в практических областях.
Прикладное значение параллельных прямых в электронике
Параллельные прямые имеют значительное прикладное значение в области электроники. Они используются для создания электрических цепей, связывающих различные компоненты и устройства.
Одно из самых распространенных применений параллельных прямых в электронике - это создание параллельного соединения компонентов. При параллельном соединении элементов электрической цепи, таких как резисторы или светодиоды, ток разделяется между ними в соответствии с правилом Кирхгофа. Это позволяет использовать несколько компонентов с одинаковыми характеристиками для увеличения суммарной мощности или яркости.
Параллельные прямые также используются в процессорах и схемах памяти для обеспечения параллельной обработки или доступа к данным. Множество проводников, расположенных параллельно друг другу, позволяют передавать данные одновременно. Это увеличивает скорость и производительность электронных устройств.
Еще одно применение параллельных прямых в электронике - это создание параллельных шин данных или адресов. В микропроцессорах и других цифровых устройствах параллельные шины используются для передачи большого количества информации одновременно, что позволяет уменьшить время передачи данных и повысить быстродействие устройства.
Кроме того, параллельные прямые используются для создания многослойных печатных плат, которые являются основой для сборки электронных устройств. Параллельные прямые, расположенные на разных слоях платы, позволяют эффективно связывать различные компоненты и установить запрограммированные соединения.
Таким образом, параллельные прямые являются важными элементами в области электроники, обеспечивая параллельное соединение компонентов, параллельную обработку данных и эффективную сборку устройств. Их использование позволяет повысить производительность, скорость и эффективность различных электронных устройств.



