Корень из 3 - одно из самых загадочных чисел в математике, которое часто встречается в различных формулах и уравнениях. Но откуда оно берется и как его можно объяснить?
Чтобы понять, откуда берется корень из 3 в формуле мощности, нужно заглянуть в мир геометрии. Корень из 3 на самом деле является результатом деления длины сторки равностороннего треугольника на длину его стороны. Этот треугольник имеет свойство, что каждая его сторона равна другой, а каждый угол равен 60 градусам. Такой треугольник является базовой фигурой для вычисления и объяснения корня из 3 в различных формулах.
Корень из 3 встречается в формуле мощности, так как он играет важную роль в вычислении работу, потребляемую электронными устройствами. Например, при вычислении мощности трёхфазных систем, корень из 3 используется для расчёта мощности в полностью сбалансированных схемах. Также этот корень активно используется при расчетах в электротехнике, тригонометрии и алгебре.
Итак, корень из 3 - это не просто случайное число, оно обладает глубоким математическим смыслом и широко применяется в различных областях. Узнав про его геометрическую основу и применение в формулах мощности, можно лучше понять его значимость и важность в нашей практической жизни.
Определение формулы мощности

Формула для расчета мощности имеет вид:
P = U * I * cos(φ)
где:
- P - мощность в ваттах;
- U - напряжение в вольтах;
- I - сила тока в амперах;
- cos(φ) - коэффициент мощности, который определяет фазовый сдвиг между напряжением и током.
В случае, когда фазовый сдвиг отсутствует и коэффициент мощности равен 1, формула упрощается:
P = U * I
Таким образом, формула мощности позволяет рассчитать энергию, потребляемую или передаваемую электроустройством при заданном напряжении и токе.
Значение мощности
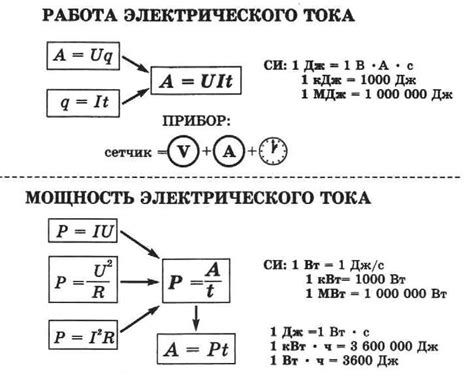
В формуле мощности P = W / t, где P обозначает мощность, W – выполненную работу, а t – время, за которое работа была выполнена. Таким образом, мощность измеряется в джоулях в секунду, или в ваттах (1 Вт = 1 Дж/с).
В случае, когда работа выполняется постоянной силой и прямолинейным движением, формула мощности имеет вид P = Fv, где F – сила, приложенная к объекту, и v – скорость перемещения объекта. В этой формуле мощность измеряется в ваттах.
Корень из 3 появляется в формуле для вычисления мощности, относящейся к трехфазным электрическим системам. В трехфазной системе мощность вычисляется по формуле P = √3 × V × I × cos(θ), где V – напряжение, I – сила тока, cos(θ) – косинус угла смещения между напряжением и током.
Фактор корня из 3

Главную роль в этом играет треугольник равносторонний, у которого все стороны равны между собой. Углы этого треугольника также равны 60 градусам. С помощью геометрических преобразований можно установить, что отношение стороны треугольника к его высоте равно корню из 3.
В формуле мощности, в которой присутствует корень из 3, возникает геометрическое отношение, связанное с силовым треугольником. В этом случае, корень из 3 возникает из отношения активной мощности к полной мощности в трехфазной системе.
Итак, корень из 3 в формуле мощности получает свое происхождение из геометрического соотношения равностороннего треугольника, где отношение стороны к высоте равно корню из 3. Это соотношение является ключевым фактором при использовании корня из 3 в формуле мощности.
Происхождение корня из 3

Учение о корне из трех в формуле мощности имеет свое происхождение в математике и физике.
В математике корень из 3 является иррациональным числом, что означает, что его десятичное представление является бесконечной десятичной дробью без периода. Впервые корень из 3 был вычислен с большой точностью древнегреческими математиками, такими как Пифагор и Евклид, которые использовали геометрические методы для нахождения этого значения.
В физике корень из 3 встречается в различных формулах, связанных с напряжением, силой тока и мощностью. Он возникает из-за комбинации разных физических величин и их единиц измерения. В частности, в формуле для расчета мощности в трифазных сетях используется коэффициент √3, который отражает соотношение между эффективным (rms) и максимальным (peak) значением напряжения или тока.
Применение корня из 3 в формулах мощности важно для правильного расчета электроэнергетических систем и схем, а также для оценки энергопотребления и эффективности различных устройств и систем.
Применение корня из 3 в формуле мощности

Формула мощности позволяет определить количество работы, которое совершается в единицу времени. В электрических цепях эта формула имеет вид:
P = VI
где P - мощность, V - напряжение, I - сила тока.
В некоторых случаях удобно вычислять мощность по другой формуле, которая выражается через эффективные значения величин:
P = Veff * Ieff
Корень из 3, появляющийся в формуле мощности, связан с тем, что эффективное значение переменного тока или напряжения составляет около 0.707 от максимального значения. Это связано с тем, что переменный ток и напряжение имеют синусоидальную форму, и эффективное значение является средним квадратическим по амплитуде величиной.
Из-за синусоидального характера переменного тока и напряжения, величины периодически повторяются. Интересующие нас параметры в электрической цепи часто выражают в комплексной форме, используя квадратный корень из 3. Кроме того, этот коэффициент участвует в преобразовании между абсолютными и комплексными значениями.
Таким образом, корень из 3 играет важную роль в формуле мощности, позволяя получить верные результаты в расчетах электрических цепей.
Расчет мощности с корнем из 3

Для рассчета мощности с корнем из 3 необходимо воспользоваться формулой:
P = U * I * sqrt(3)
Где:
P - мощность в трехфазной системе;
U - напряжение между фазами;
I - сила тока;
sqrt(3) - квадратный корень из 3, который нужно умножить на произведение напряжения и силы тока для получения корректной мощности.
Такая формула используется для расчета мощности в трехфазных электрических системах, где применяется симметричная нагрузка и углы между фазами составляют 120 градусов.
Учет квадратного корня из 3 позволяет учесть взаимодействие между фазами и получить более точное значение мощности в трехфазной системе.



