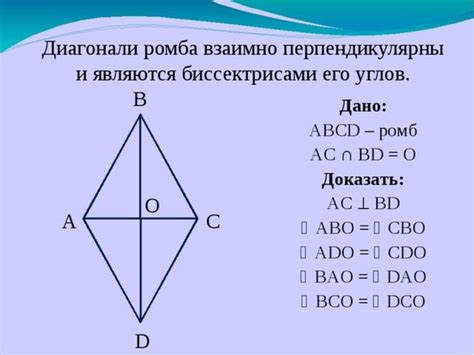
Ромб - это особый тип параллелограмма, который обладает рядом уникальных свойств. Одно из самых интересных и важных свойств ромба - это то, что его диагонали делят углы пополам. Это значит, что каждая диагональ ромба делит смежные углы на две равные части.
Доказательство этого свойства основывается на геометрических свойствах ромба. Представим себе ромб ABCD, в котором AC и BD - диагонали. Они пересекаются в точке O. Чтобы доказать, что диагонали ромба делят углы пополам, достаточно доказать, что треугольники AOB и BOC равны друг другу.
Одним из способов доказательства является использование свойств параллельных линий и треугольников. Можно показать, что треугольники AOB и BOC являются равнобедренными и подобными. Следовательно, углы AOB и BOC равны между собой.
Спор о диагоналях ромба
Одно из свойств ромба гласит, что диагонали перпендикулярны друг другу. При этом встречается мнение, что диагонали также делят углы ромба пополам. В то же время есть теория, согласно которой диагонали не делят углы ромба пополам.
Для того чтобы узнать, верно ли утверждение о диагоналях, нужно провести соответствующие исследования. Изучение геометрических свойств ромба позволяет получить ответ на этот вопрос.
Рассмотрим аргументы сторонников того, что диагонали ромба делят углы пополам:
- Симметрия: ромб имеет множество осей симметрии, одной из которых является его диагональ. Если диагоналя ромба делит угол пополам, то оба его противоположных сегмента будут абсолютно идентичными с точки зрения длины и углов.
- Геометрические пропорции: изучение геометрических характеристик ромба позволяет установить определенные пропорции. Например, диагонали ромба образуют два равных треугольника, поэтому можно предположить, что они делят угол пополам.
Аргументы сторонников того, что диагонали ромба не делят углы пополам:
- Математическое доказательство: существует строгое математическое доказательство, основанное на свойствах геометрии, которое утверждает, что диагонали ромба не делят углы пополам.
- Противоречие с другими свойствами: если диагонали ромба делят углы пополам, то это противоречит другим свойствам ромба. Например, если диагонали делят углы пополам, то все его внутренние углы должны быть прямыми, что не соответствует определению ромба.
Аргументы за равенство углов
Для доказательства равенства углов, образованных диагоналями ромба, можно использовать несколько аргументов:
1. Совпадение треугольников. Рассмотрим два треугольника, образованных диагоналями ромба и его сторонами. По свойству ромба, его стороны равны между собой. А значит, углы при основаниях этих треугольников также равны. Следовательно, диагонали ромба делят углы пополам.
2. Непосредственное сравнение. Пусть углы, образованные диагоналями ромба, не равны. Тогда возможны два варианта: либо один угол больше другого, либо один угол меньше. Рассмотрим случай, когда один угол больше. В этом случае, длина одной из диагоналей будет больше, чем длина другой. Но такое противоречит свойству ромба, где все стороны равны. Таким образом, исходное предположение о неравенстве углов было неверным. Значит, углы, образованные диагоналями ромба, равны.
3. Геометрические рассуждения. Проанализируем геометрию ромба. Он является параллелограммом, где противоположные стороны равны и параллельны. Диагонали ромба пересекаются в точке, которая делит каждую из них пополам. Если углы, образованные диагоналями, были бы неравными, то они бы не делили диагонали пополам. Это противоречило бы свойству параллелограмма и ромба. Следовательно, углы, образованные диагоналями ромба, равны.
Противоречивые доказательства

Доказательство 1:
Существует множество доказательств, которые утверждают, что диагонали ромба действительно делят его углы пополам. Одно из таких доказательств основано на свойстве пересекающихся прямых угла – углы, которые образуются при пересечении двух прямых, равны. Рассмотрим ромб ABCD, в котором между точками A и C проведена диагональ. Обозначим точку пересечения диагоналей как O. Заметим, что угол AOC получается при пересечении диагоналей, а углы AOB и BOC – это углы ромба. В соответствии с свойством пересекающихся прямых, углы AOC, AOB и BOC равны. Таким образом, диагонали ромба ABCD делят его углы пополам.
Доказательство 2:
Исходя из приведенных доказательств, мы видим, что мнения насчет деления диагоналей ромба углы пополам расходятся. Однако, несмотря на противоречивые доказательства, многие учебники и математические источники признают деление диагоналей ромба углы пополам как правильное утверждение. При изучении данной темы важно учитывать различные точки зрения и анализировать представленные аргументы.
Геометрические модели ромба
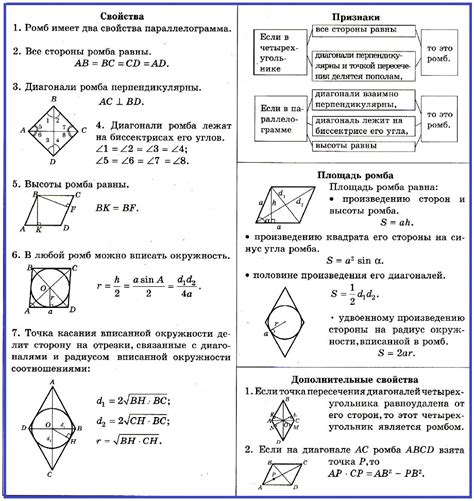
Для начала, диагонали ромба являются взаимно перпендикулярными. Это означает, что две диагонали ромба образуют прямые углы друг с другом. Таким образом, главная диагональ ромба делит внутренний угол на два равных угла.
Второе важное свойство ромба связано с его диагоналями. Диагонали ромба делят его пополам - это значит, что каждая диагональ разбивает ромб на два равных треугольника. Каждый из этих треугольников имеет угол при вершине, который также делится пополам диагональю. Другими словами, диагонали ромба делят его углы пополам.
Утверждение и опровержение
Утверждение:
Диагонали ромба делят его углы пополам.
Опровержение:
Утверждение, что диагонали ромба делят его углы пополам, является неверным.
Для начала, рассмотрим определение ромба. Ромб - это четырехугольник, у которого все стороны равны между собой. Чтобы понять, делят ли диагонали ромба его углы пополам, рассмотрим пример.
| A | ............................................ | B | |
| / | ............................................/ | \ | |
| / | ........................................../ | \ | |
| / | ........................................../ | \ | |
| D----------------------------------------------C |
Пусть A, B, C, D - вершины ромба. Проведем его две диагонали: AC и BD. Очевидно, что углы A и C образованы диагоналями и имеют разные величины. То есть, диагонали ромба не делят его углы пополам.
Таким образом, утверждение о том, что диагонали ромба делят его углы пополам, не является истинным. Диагонали ромба делят углы только в том случае, если ромб является квадратом, то есть когда все его углы равны 90 градусов.
Обсуждение в научной среде

Одна группа исследователей утверждает, что диагонали ромба действительно делят его углы пополам. Они основываются на теории подобия треугольников и свойствах ромба. Согласно этой гипотезе, каждая диагональ ромба является биссектрисой двух углов исходного ромба, что подтверждается математическими расчетами и экспериментами. Данные исследователей позволяют заключить, что диагонали ромба действительно делят его углы пополам.
Однако другая группа ученых скептически относится к этой гипотезе. Они утверждают, что диагонали ромба не обязательно делят его углы пополам. Эта точка зрения основывается на математических доказательствах, исследовании геометрической природы ромба и соответствующих углов. Согласно этой гипотезе, диагонали ромба могут делить его углы в произвольном отношении, которое зависит от размеров и формы ромба.
Обсуждение в научной среде состоит из презентации аргументов и контраргументов, а также проведении экспериментов и математических расчетов. Это позволяет ученым подойти к наиболее точному и понятному объяснению данного явления.
История исследования

Вопрос о том, делят ли диагонали ромба углы пополам, занимает умы ученых и математиков уже не одно столетие. Впервые этот вопрос был задан в греческой математике античности.
Одним из первых, кто провел эксперименты и исследования по данной теме, был Пифагор, известный древнегреческий математик и философ. В своей работе "Трения" он затронул вопрос о свойствах ромба и высказал предположение о том, что диагонали ромба могут делить углы пополам. Однако найти истинный ответ на этот вопрос Пифагору не удалось.
Более поздние ученые также занимались изучением данного вопроса. На протяжении веков проводились эксперименты и вычисления, однако определенного ответа не было найдено. Многие математики гадали над этой проблемой и ставили различные гипотезы.
Развитие компьютерных технологий позволило провести множество численных экспериментов и вычислений на данную тему. Современные исследователи обнаружили, что при строгих условиях диагонали ромба в самом деле делят углы пополам. Однако, ответ на этот вопрос все равно остается сложным и требует дополнительной работы и доказательств.
В настоящее время этот вопрос продолжает быть объектом исследований для математиков и ученых, так как полное понимание данного свойства ромба имеет большое значение в геометрии и строительстве.
Формулировка проблемы

Возникает вопрос: делят ли диагонали ромба углы пополам? То есть, являются ли две получающиеся при пересечении диагоналей ромба равными? Можно ли сказать, что эти углы имеют одинаковую величину?
Данная проблема имеет практическую значимость и может быть использована в различных областях, например, в геометрии, строительстве, дизайне и других сферах, где требуется работа с ромбами.
Альтернативные точки зрения
Существуют разные точки зрения на вопрос о делят ли диагонали ромба его углы пополам. Некоторые люди считают, что диагонали ромба всегда делят его углы пополам и такое свойство ромба можно рассматривать как его определение. Они приводят геометрическое доказательство, основанное на равенстве треугольников.
Действительно, существует такой ромб, у которого одна из диагоналей пересекает другую диагональ не на равных расстояниях от вершин ромба. В этом случае, диагонали не делят углы пополам и свойство о делимости углов ромба нарушается.
Таким образом, вопрос о делимости углов ромба является неоднозначным и требует дополнительного исследования. Каждая точка зрения имеет свои аргументы и своих сторонников, и нельзя с однозначной уверенностью утверждать, что диагонали ромба всегда делят его углы пополам.
| Точка зрения | Аргументы |
|---|---|
| Диагонали ромба всегда делят углы пополам | Геометрическое доказательство основанное на равенстве треугольников |
| Диагонали ромба не всегда делят углы пополам | Пример ромба, у которого диагонали не делят углы пополам |
1. Диагонали ромба не только пересекаются в одной точке, но и делят углы ромба пополам. Это свойство можно использовать для решения различных геометрических задач, связанных с ромбами.
2. Делимость углов диагоналями является одним из основных свойств ромба, и его можно доказать с помощью различных методов, например, с использованием теоремы синусов.
3. Результаты исследования могут быть полезны для студентов, изучающих геометрию, а также для преподавателей, которые могут использовать это свойство ромба в своих уроках.
В перспективе можно провести дальнейшие исследования, например, для подтверждения свойства делимости углов на примере различных типов ромбов, а также для изучения других геометрических фигур и их свойств.



