Производная – это одно из ключевых понятий математического анализа, которое нашло широкое применение в различных областях науки и техники. Она позволяет нам изучать изменение функций, исследовать экстремумы, определять скорость изменения величин и многое другое.
В данной статье мы рассмотрим основные принципы работы с производными, а также рассмотрим конкретные примеры их применения в реальной жизни. Математические методы, основанные на производных, позволяют решать разнообразные задачи, связанные с оптимизацией процессов, моделированием динамики систем и прогнозированием различных явлений.
Благодаря пониманию основных принципов производных и умению применять их на практике, мы можем значительно улучшить понимание окружающего мира и повысить эффективность наших действий в различных областях деятельности.
Важность производной в повседневной жизни

Важность производной проявляется во многих сферах нашей жизни, начиная от финансового планирования и управления ресурсами до оценки изменений в окружающей среде и развития технологий. Например, в экономике производная может использоваться для прогнозирования роста компании и определения оптимальных стратегий управления. В физике производная помогает анализировать движение тела, в биологии - развитие организмов, а в информационных технологиях - улучшение алгоритмов и программ.
Таким образом, знание и применение производной помогает нам лучше понимать окружающий мир, принимать обоснованные решения и улучшать качество жизни. Поэтому важно осознавать значение этого математического инструмента и развивать навыки его использования для достижения успеха в различных областях деятельности.
Преимущества изучения производной

Изучение производной имеет множество преимуществ и практические применения в различных областях жизни. Ниже представлены основные преимущества изучения производной:
| 1. | Ускорение процессов оптимизации: производная позволяет найти точки экстремума функций, что помогает в улучшении эффективности процессов в различных сферах деятельности. |
| 2. | Повышение точности прогнозирования: анализ производной позволяет предсказывать тенденции и изменения в данных, что полезно при принятии стратегических решений. |
| 3. | Улучшение понимания процессов и явлений: производная помогает интерпретировать форму и поведение функций, что способствует глубокому пониманию и исследованию различных явлений. |
| 4. | Развитие аналитических навыков: изучение производной требует аналитического мышления и логического рассуждения, что способствует развитию способности к анализу и решению сложных задач. |
Функциональное применение производной

Одним из ключевых применений производной является определение скорости изменения величины. Например, если функция задает зависимость пути от времени, то производная этой функции позволяет найти мгновенную скорость движения в каждый момент времени. Это имеет применение в физике, экономике, биологии и других областях.
Применение производной в финансовой сфере

Математические концепции, такие как производная, играют ключевую роль в финансовой сфере. Они помогают анализировать и прогнозировать изменения в экономике, ценах акций, доходах компаний и многом другом. Вот несколько примеров использования производной в финансах:
- Оценка рисков: Производная позволяет вычислять показатели, связанные с риском инвестиций. Например, бета-коэффициент - это производная, которая помогает инвесторам оценить изменчивость цены акции по сравнению с индексом рынка.
- Моделирование цен: Производная используется для создания математических моделей, предсказывающих движение цен на финансовых рынках. Например, модели Блэка-Шоулза используют производные для определения цены опциона.
- Управление портфелем: Производные помогают анализировать доходность портфеля активов, определять оптимальные стратегии инвестирования и минимизировать риски.
Использование производной в финансах помогает инвесторам, аналитикам и управляющим рисками принимать обоснованные решения, основанные на математических методах и моделях.
Производная в технических задачах

Производные имеют широкое применение в решении различных технических задач. Например, в механике они используются для определения скорости и ускорения тела. Путем взятия производной пути по времени можно найти скорость движения объекта в каждый момент времени.
Также производные применяются в электротехнике для анализа переменного тока, при построении фильтров и усилителей. Использование производных позволяет более точно моделировать и предсказывать поведение электрических цепей.
В строительстве и архитектуре производные используются для оптимизации формы и конструкции сооружений. Например, при проектировании мостов или зданий, производные помогают учитывать нагрузки, распределение массы и прочие факторы, чтобы обеспечить максимальную прочность и эффективность конструкции.
Интересные примеры использования производной
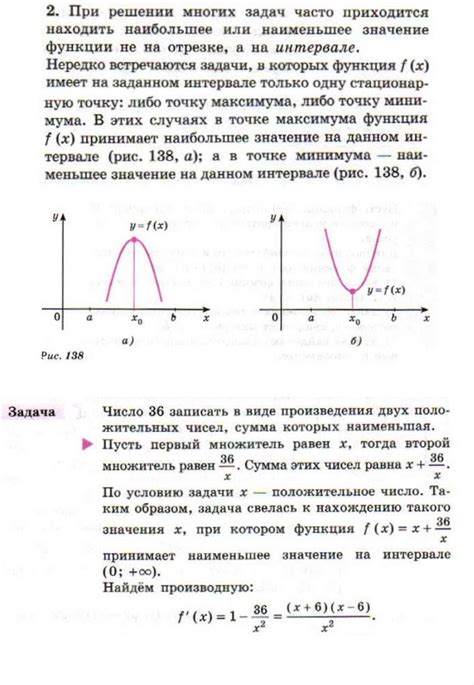
2. Оптимизация: для поиска экстремумов функций используются производные, например, для определения максимальной площади огороженного участка.
3. Физика: производная плотности массы по объему дает плотность распределения массы в пространстве.
4. Экономика: производная спроса показывает изменение спроса в зависимости от цены товаров.
5. Инженерия: производные используются при проектировании строительных конструкций, например, для расчета деформаций или сил в элементах конструкции.
Вопрос-ответ

Зачем нужно применять производные в жизни?
Применение производных в жизни позволяет решать задачи оптимизации, то есть находить экстремумы функций, что помогает принимать более эффективные решения. Например, производные используются в экономике для определения максимального дохода или минимальных издержек при производстве. Также производные применяются в физике для нахождения скорости, ускорения и других параметров движения тел.
Какое практическое применение производных можно привести в обыденной жизни?
Применение производных можно увидеть во многих сферах обыденной жизни. Например, при проектировании автомобилей или любых других механизмов используются производные для оптимизации работоспособности и безопасности. Также производные применяются в фармакологии для определения оптимальной дозировки лекарств. Даже при планировании путешествий производные могут быть использованы для оптимизации времени и дистанций.